
「Petrozavodsk Summer 2020」Parity Sort
一月 21, 2021 · OI 题解
定义一个排列 $P$ 上的操作 $(t,S)$ 为:
- 有两个空序列 $A$ 和 $B$
- 枚举 $i$ 从 $1$ 到 $n$
- 如果 $S_i=0$,不进行操作
- 如果 $S_i=1$,如果 $P_i$ 是偶数,则放到 $A$ 的末尾,否则放到 $B$ 的末尾
- 如果 $t=0$,$C=\overline{AB}$;否则 $C=\overline{BA}$。
- 枚举 $i$ 从 $1$ 到 $n$
- 如果 $S_i=0$,不进行操作
- 如果 $S_i=1$,将 $P_i$ 设为 $C$ 的开头元素,删去 $C$ 的开头元素
现给出一个排列 $P$,你需要使用至多 $30$ 次如上操作,使 $P$ 从小到大排序,注意你并不需要最小化操作次数。
$1\le n\le 15000$。
题意补充
对于 $P=\{0,4,2,3,6,5,1\}$ 上的操作 $(1,\texttt{1101101})$,有示意图如下
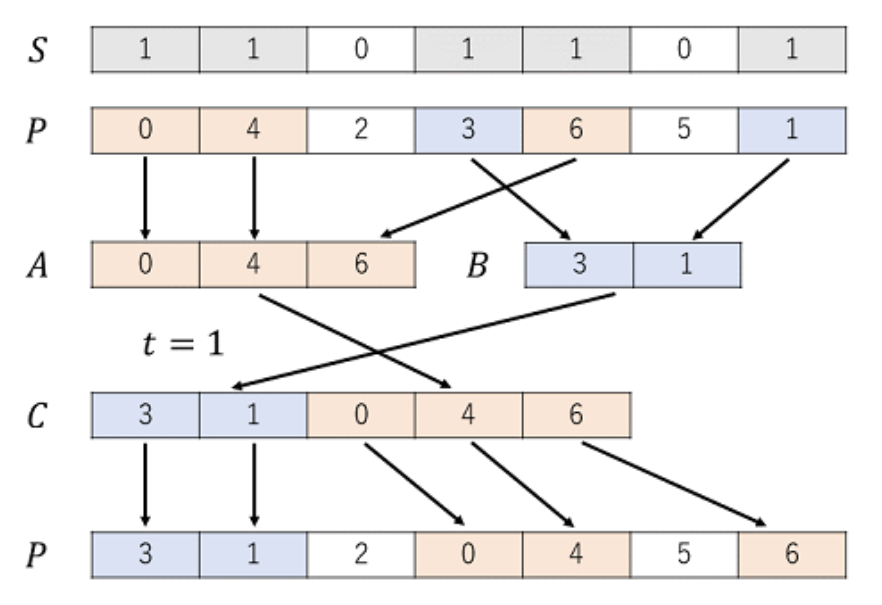
题解
由于 $30=2\left(\left\lfloor\log n\right\rfloor\right)+1$,我们考虑 $t=0$ 和 $t=1$ 的操作交错执行。
首先可以确定最后一次操作前,每个数的位置,如 $n=13$ 的时候,最后一次操作前的 $p$ 应为:
1 | 0 8 2 10 4 12 6 7 1 9 3 11 5 |
故对于每个数,我们求出此时期望的位置 $rk$,也就是说,现在我们要把每个 $p_i$,移动到 $rk_{p_i}$ 的位置上。
考虑从低位到高位,每次把这一位是 $1$ 的数不改变相对顺序地丢到最后面,$\log$ 次后即可完成排序。
先进行一次 $(0,\texttt{111\ldots1})$ 操作后,所有偶数都在奇数前面,我们可以认为是两个序列;把偶数中需要放后面的数和奇数中需要放前面的数执行 $t=1$ 操作即可。但 $n$ 时可能两侧的数字个数不同,这时候给偶数序列中多丢一个 $0$ 就好了。
代码
1 |
|