根号数据结构复习

分块，可以看做一个度数为 $\sqrt n$，只有三层的树。

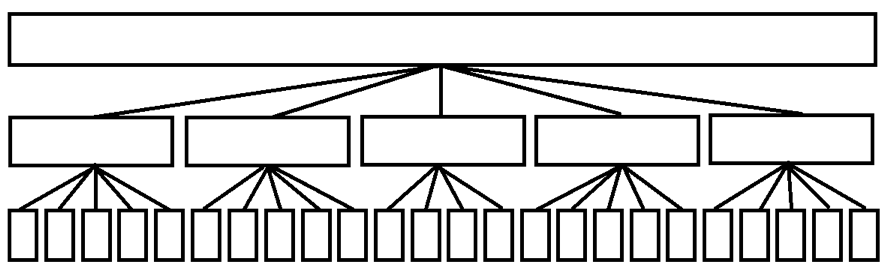
所以如果在分治结构上很难快速合并某些信息，我们就可以利用分块来做。

动态分块

0x01 经典问题

维护一个序列，支持：1.区间加；2.查询区间小于 $x$ 的数个数。

块大小为 $\sqrt {n \log n}$ 分块，可以做到 $O(m \sqrt {n \log n})$ 的复杂度。

0x02 [Ynoi2017]舌尖上的由乃

维护一个序列，支持：1.区间加；2.查询区间第 $k$ 小。

显然需要二分。块大小设置为 $\sqrt n \log n$，二分开始前把两个零散块拼起来。时间复杂度 $O(m \sqrt n \log n)$

用根号平衡来优化数据结构复杂度

0x01

维护一个序列，支持：1. $O(1)$ 单点修改；2. $O(\sqrt n)$ 区间和。

修改

查询

0x02

维护一个序列，支持：1. $O(\sqrt n)$ 单点修改；2. $O(1)$ 区间和。

维护前缀和。

修改

查询

0x03

维护一个序列，支持：1. $O(\sqrt n)$ 区间加；2. $O(1)$ 查单点。

修改

查询

0x04

维护一个序列，支持：1. $O(1)$ 区间加；2. $O(\sqrt n)$ 查单点。

差分。

修改

查询

0x05

维护一个集合，支持：1. $O(1)$ 插入一个数；2. $O(\sqrt n)$ 查询第 $k$ 小。值域与 $n$ 同阶。

修改

查询：最多跨过 $\sqrt n$ 个整块和 $\sqrt n$ 个零散的数。

0x06

维护一个集合，支持：1. $O(\sqrt n)$ 插入一个数；2. $O(1)$ 查询第 $k$ 小。值域与 $n$ 同阶。

直接维护一下整个队列，把整个队列分块。

插入一个数的时候重构一下对应的队列，如果队列超了就把最后的数丟到下一个块。

修改

查询

0x07 CodeChef Chef and Churu

给 $n$ 个数，给定 $m$ 函数，每个函数为序列中第 $l_i$ 到第 $r_i$ 个数的和。有 $q$ 个两种类型的操作：

1. 1 x y 把序列中第 $x$ 个数改成 $y$
2. 2 x y 求第 $x$ 个函数到第 $y$ 个函数的和

把 $m$ 个函数分块。整块的可以直接维护，零散块用一个 $O(\sqrt n)$ 修改，$O(1)$ 查询的分块维护。

简单莫队算法

常见优化

• 奇偶块排序，可以快一倍左右。
• 调整块大小 $\left( n / \sqrt { 2m / 3 } \right)$ 可以快 $10\%$ 左右。

0x01 [AHOI2013]作业

给定序列，支持查询区间 $[l,r]$ 中值在 $[a,b]$ 内的不同数个数。

$n \leq 10^5,\ m \leq 10^6$。

序列离散化，跑一个莫队。拉一个 $O(1)$ 插入，$O(\sqrt n)$ 求和的分块即可。时间复杂度 $O(m \sqrt n)$。

另外显然有 polylog 做法（话说我第一反应也是 polylog（（（

0x02 [Ynoi2016]这是我自己的发明

给一个树，有点权，初始根是 $1$。支持：

• 1 x：将树根换为 $x$
• 2 x y：从 $x$ 的子树中选每一个点，$y$ 的子树中选每一个点，如果两个点点权相等则ans++，求 $ans$。

考虑把树上换根问子树转化到序列上。每次询问有四个参数不好维护，可以差分成四个询问每次两个参数：

$$F(l_1,r_1,l_2,r_2)=F(1,r_1,1,r_2)-F(1,l_1-1,1,r_2)-F(1,r_1,1,l2-1)+F(1,l_1-1,1,l2-1)$$

注意这里询问次数可能会比较多，可以考虑基数排序询问。时间复杂度 $O(n \sqrt m + m)$。

0x03 BZOJ3920 Yunna的礼物

给定序列，支持查询区间中出现次数 $k_1$ 小的数里面的 $k_2$ 小的数。卡空间。

考虑一种高维离散化技巧，以出现次数为第一关键字，数值为第二关键字排序，仍是 $O(n)$ 项的。

然后一边跑一个莫队，用一个 $O(1)$ 修改，$O(\sqrt n)$ 查询值域分块来维护就好。

时间复杂度 $O(m \sqrt n)$。

0x04 BZOJ4241 历史研究

给定序列，定义 $\operatorname{Chtholly}(l,r,x)$ 为 $x$ 在区间 $[l,r]$ 中出现次数，支持查询一个区间中最大的 $x \times \operatorname{Chtholly}(l,r,x)$。

用上一题的方法离散化后莫队维护即可。时间复杂度 $O(m \sqrt n)$。

0x04 [Ynoi2015]纵使日薄西山

给定序列，定义区间 $[l,r]$ 的贡献为其每一个子序列贡献和；定义子序列 $\alpha$ 的贡献为 $\alpha$ 内的元素去重后的和。支持查询区间贡献。

考虑数 $x$ 在长度为 $l$ 的区间中出现了 $y$ 次，贡献为：

$$x \times 2^{l - y} \times (2^{y} - 1) = x (2 ^ l - 2 ^ {l - y})$$

可以分成两部分计算。第一部分是好维护的，第二部分可以把 $y$ 相同的放在一起计算。其中 $y$ 不同的至多只有 $O(\sqrt l)$ 个。

为了 $O(1)$ 算出快速幂，我们可以预处理出 $2^{1}, 2^2 , … , 2^{\sqrt n}$ 和 $2^{\sqrt n} , 2^{2 \sqrt n} , … , 2^{\sqrt n \sqrt n}$。（类似分块打表的思想）

0x05 [HNOI2016]大数

给定一个数字串和质数 $p$，支持查询这个数字串的一个子串里有多少个子串是 $p$ 的倍数。

首先处理掉 $p=2$ 或 $p=5$ 的情况。然后考虑子串 $[l,r]$ 是 $p$ 的倍数当且仅当 $s_{l-1} \equiv s_{r} \pmod p$。

离散化后等价于小 Z 的袜子。

0x06 区间逆序对

给定序列，支持查询区间逆序对个数。

Solution 1

把值域分块的结构可持久化（lxl 称为可持久化块状树），插入+可持久化的复杂度 $O(\sqrt n)$，查询的复杂度 $O(1)$。

结合经典的莫队做法可以做到 $O(n \sqrt m)$ 的时间复杂度和 $O(n \sqrt n)$ 的空间复杂度。

Solution 2

莫队二次离线：
将莫队当做是 $O( n \sqrt m )$ 次查询区间中满足特定特征的性质的数的某个信息。
如果这个信息具有可减性，可以差分。
考虑差分后变成 $O( n \sqrt m )$ 次查询前缀中满足特定特征的性质的数的某个信息。

一个暴力的维护方式是：

每次我们从 $[l,r]$ 转移到 $[l,r-1]$ 或 $[l,r+1]$ 或 $[l-1,r]$ 或 $[l+1,r]$ 的时候，假设要求的是区间小于 $z$ 的数的个数。
那么就差分一下，在 $l-1$ 处打上标记 $(x,-z)$，在 $r$ 处打上标记 $(x,z)$。

然后扫一遍，用值域分块维护就可以 $O(1)$ 知道每次转移的贡献了。

时间复杂度 $O(n \sqrt m)$，空间复杂度 $O(\sqrt m)$（自带两倍常数）。

由于空间常数巨大，寻址不连续，这是一个空间和时间都消耗巨大的算法。我们考虑从空间入手优化。

致谢

nzhtl1477 的讲课。